Вектори и операции с вектори

Стандартната определението на "вектор - целеви сегмент". Обикновено това са ограничени и завършил знания на вектори. Кой се нуждае от някои ", насочени сегменти?

И всъщност, че такива вектори, и защо да го правят?
Прогноза за времето. "Вятър СЗ, скорост 18 метра в секунда." Приемам, че има големина и посока на вятъра (когато вятърът духа), и модул (т.е., абсолютната стойност на) скорост.

Стойностите не са с посока, наречена скаларна. Маса, работа, електрически заряд, няма да е указано. Те се характеризират с числена стойност - ". Колко джаула" "колко килограма" или

Физични величини, които имат не само абсолютната стойност, но и посоката се нарича вектор.

Скорост, сила, ускорение - вектори. За тях е важно да се "колко" и важно ", където". Например, гравитационното ускорение е насочен към земната повърхност, и неговата стойност е равна на 9.8 m / и 2. импулс електрическо поле, магнитното поле - същия вектор количества.

Ще си спомните, че физически количества, са обозначени с буквите, латино или гръцки. Стрелката над писмото показва, че големината на вектора е:

Ето още един пример.
движи на автомобили от А до точка Б. крайният резултат - тя се премества от точка А до точка Б. движение т.е. вектор.

Сега разбирам защо вектора - целеви сегмент. Моля, обърнете внимание, в края на вектора - когато стрелката. Дължината на вектора е дължината на този сегмент. Означени: или

Досега сме работили с скаларни стойности, в съответствие с правилата на аритметиката и елементарна алгебра. Вектори - нова концепция. Това е различен клас математически обекти. За тях правилата.

След като и броят не знаеше нищо. Запознаване с тях започна в ранните класове. Установено е, че цифрите могат да се сравняват един с друг, събиране, изваждане, умножение и деление. Научихме, че има определен брой елементи, а цифрата нула.
Сега ние се въвеждат с вектори.

"По-малко от" вектори не съществуват понятията "повече" и - поради тяхната посока може да бъде различна. Можете да сравните само дължината на векторите.

Но идеята за равенство за вектори там.
Равен е вектор със същата дължина и съща посока. Това означава, че векторът може да бъде прехвърлен успоредно на себе си във всяка точка на самолета.
Устройството е вектор, чиято дължина е равна на нула 1. - вектор, чиято дължина е равна на нула, т.е. неговия произход съвпада с края.

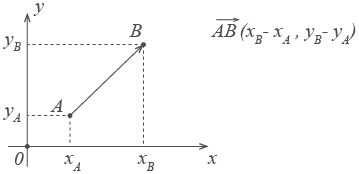
Най-удобният начин за работа с вектори в Декартова координатна система - същата, в която изтеглящите графиките на функции. Всяка точка в координатната система съответства на две числа - координатите х и у. абсциса и ордината.






Векторът също се определя от две координати:

Тук в скоби записва координати на вектора - за х и у.
Те са просто: Координиране на края на вектора минус координира неговото начало.

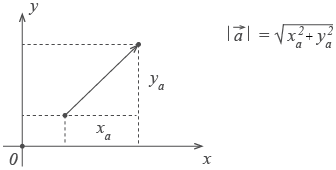
Ако не са посочени координатите на вектора, дължината му е дадено от

добавяне на вектори

За допълнение вектор има два начина.

1. Върховенство на успоредник. За да сгънете вектори и сложи двете старт в една точка. За да се завърши изграждането на успоредник и съща точка на диагонала на успоредника изпълни. Това ще бъде сумата от вектори.

Не забравяйте, баснята за лебед, рак и щука? Те се опитаха много трудно, но не помръдна от мястото на СЗО. След вектор сборът на силите, прилагани от тях в колата, тя е равна на нула.

2. Вторият метод на добавяне на вектори - обикновено триъгълници. Вземете същите вектори. До края на първия вектор да прикачите началото на втория. Сега се комбинират в началото на първия и втория край. Това е сумата на векторите.

По същото правило може да се сгъне и няколко вектори. За да ги прилага един по един, а след това се свържете с началото на първия края на последния.

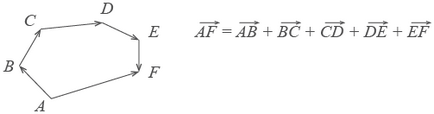
Представете си, че да отидеш от точка А до точка Б. от B до C от C до D. тогава Е и F. крайният резултат от тези действия на - движи от точка А до F.

При добавяне на вектори, и получаваме:

изваждане на вектори

Вектор е насочен противоположно на вектора. Дължините на вектори и са равни.

Сега е ясно, че това изваждане на вектори. Векторите разликата и - това е сумата на вектора и вектора.

Умножение на вектор от редица

Когато се умножи по броя на вектор К е вектор с дължина к във времето се различава от дължината. Той има една и съща посока с вектора, ако к е по-голяма от нула, и е насочено срещу, ако к е по-малка от нула.

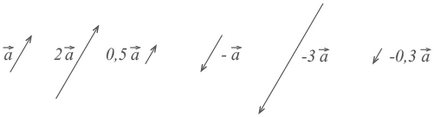
Ти намери това, което търсите? Споделете с приятелите си!

В скаларен продукт на два вектора

Вектори могат да се умножат не само в цифри, но и в един от друг.

Скаларно произведение е продукт на дължините на векторите на косинуса на ъгъла между тях.

Моля, имайте предвид - да се размножават два вектора, скаларни и се обърна, че е броя. Например, в областта на физиката, механична работа е равна на скаларен продукт на два вектора - силите и движения:

Ако векторите са перпендикулярни, тяхното скаларен продукт е нула.
И това се изразява чрез скаларно произведение на вектори и координати:

Можете да намерите на ъгъла между векторите от формулата за вътрешния продукт:

Тази формула е особено полезно в твърда геометрия. Например, в проблема на С2 е необходимо да се намери на ъгъла между права или кос между права и равнина. Често, вектор метод С2 проблем е решен в рамките на няколко пъти по-бързо от класиката.

Учебната програма за училище по математика проучване само скаларно произведение на вектори.
Оказва се, с изключение на скаларна, има също вектор продукт, в резултат на размножаването на два вектора е вектор. Кой доставя на изпит по физика. знае какво силата на Лоренц и силата на Ампер. Формулата за намиране на тези сили са именно векторни продукти.

Вектори - полезен математически инструмент. В това ще видите в първата година.

Обадете ни се: 8 (800) 775-06-82 (безплатно обаждане на България) +7 (495) 984-09-27 (безплатно обаждане в Москва)

Или щракнете върху връзката "Научете повече", за да попълните формата за контакт. Ние определено ще ви се обадим.