Вектори и операции с вектори

Вектори заемат специално място сред обектите разглеждат висша математика, тъй като всеки вектор има не само числова стойност - дължината, но и физическото и геометрична - ориентация. Векторът, представено чрез насочена отсечка, простираща се от точка А до точка В. обозначен с.

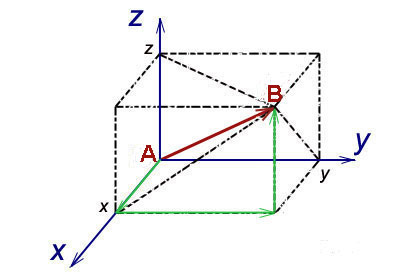
Вектор - вид представяне на точката за който се изисква достъп от някои начална точка. Например, триизмерна вектор, обикновено в писмена форма (X, Y, Z). Говорейки съвсем просто, тези числа означават, колко далеч искате да отидете в три различни посоки, за да стигнем до точката.

При един вектор. Където х = 3 (дясната ръка сочи надясно), у = 1 (лявата ръка сочи напред), Z = 5 (точка стои под стълбите водещи). От тези данни ще намерите точка на преминаване от 3 метра в посоката, указана от дясната ръка, след това 1 метър в посока на лявата ръка, а след това се чака една стълба и се изкачва на 5 метра, най-накрая свърши в желаната точка.

Всички други условия - по-точно обяснение, представена по-горе, необходими за различни операции на вектори, т.е. решаването на практически проблеми. Разходка в този по-строг дефиниция, позовавайки се на типичните задачи на вектори.

Физични примери на векторни количества могат да служат като изместване на материална точка, се движи в пространството, скорост и ускорение на този момент, както и качеството на силата на него.

Геометричната вектор е представена в двумерен и триизмерното пространство като насочена отсечка. т.е. сегмент, който се прави разлика в началото и края.

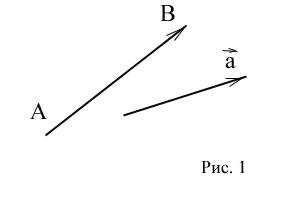
Ако А - началото на вектора, и В - край, векторът обозначен с един или малка буква. Фигурата показва края на вектор стрелка (фиг. 1)

Дължина (или модул) е дължината на геометричната вектор генериране дължината

Две вектори се казва, че са равни. ако те могат да се комбинират (в съвпадение посоки) от паралелно предаване, т.е. ако те са успоредни, те са насочени към една и съща посока и имат еднаква дължина.

Във физиката, често се счита, залегнали вектори. предварително определена точка на прилагане, дължина и посока. Ако точката на прилагане на вектора не е от значение, може да се прехвърля, като същевременно се поддържа дължината и посоката във всяка точка в пространството. В този случай, вектора се нарича безплатно. Ние сме съгласни да се разгледа само безплатни вектори.

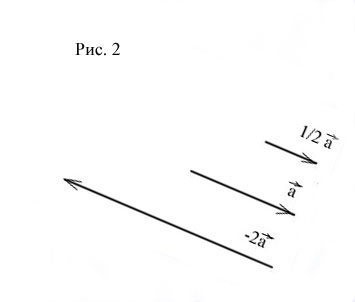
Умножение на вектор от редица

номер Vektorana продукт е вектор, получен от вектора разтягане (If) или свиване (а) във времето, с посоката на вектора записан ако и обратно, ако. (Фиг. 2)

От определението следва, че векторите ф винаги намира на същата или на успоредни линии. Такива вектори се наричат ​​колинеарни. (Можете също да се каже, че тези вектори са паралелни, но вектор смятане да се каже "лежат".) Обратното също е вярно: ако векторите и лежат на една права, то те са свързани с

Следователно, уравнение (1) изразява състоянието на колинеарност на два вектора.

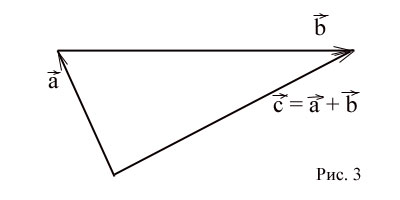
Събиране и изваждане на вектори

При добавяне на вектори трябва да знаят, че сумата на векторите е вектор, началото на която съвпада с началото на вектора, а в края - до края на вектора, при условие, че произходът на вектора се прилага до края на вектора. (Фиг. 3)

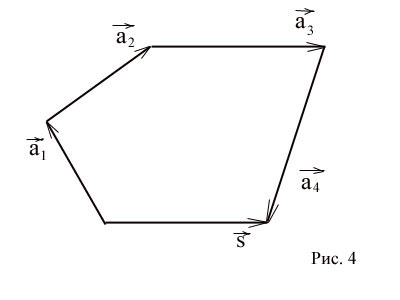
Това определение може да се разпространява и да е краен брой вектори. В пространство п са свободни вектори. При добавяне на няколко вектори за вземане на тяхната сума NO вектор, чиито начало съвпада с началото на първия вектор, а в края - края на последния вектор. Това означава, че ако до края на вектора да направи старт вектор и края на вектора - началото на вектора и т.н. и, накрая, до края на вектора - началото на вектора, сумата от тези вектори се затваря вектор, началото на която съвпада с началото на първия вектор и края - края на миналата вектор. (Фиг. 4)

Условията са наречени елементи на вектора, и формулирани правило - принципа на многоъгълника. Този полигон не може да бъде гладка.

Когато бъде умножен по броя на вектори получени -1 срещу вектор. Вектори имат еднаква дължина и в противоположни посоки. Тяхната сума дава вектор нула. чиято дължина е равна на нула. нула посока вектор не е определен.

В вектор алгебра не трябва да се разглеждат поотделно изваждане: изважда от вектора означава вектор добавя към противоположния вектора на вектор, т.е.

Пример 1: Опростяване на израза:

т.е., могат да се добавят и вектори, умножена по броя както полиноми (по-специално, проблемът е да се опрости изразите). Обикновено, необходимостта да се опрости линейни изрази такива вектори възниква преди изчисляване на продукти от вектори.

Пример 2. Вектори и служи диагоналите на ABCD на успоредник (Фиг. 4а). Изразени по отношение на векторите, и които са страни по този успоредник.

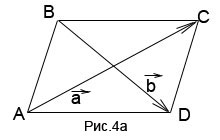
Решение. Пресечната точка на диагоналите на успоредник разделя всяка диагонална половина. Дължините на желани вектори са или и двете половинки сума вектори, образуващи триъгълник с желания или като половината от разликата (в зависимост от посоката на обслужващи диагонал), или, в последния случай, половината количество, взети със знак минус. Следователно, необходими вектори са:

Как да се намери дължината на сумата на векторите?

Този проблем има специално място в операциите с вектори, тъй като предполага използването на тригонометричните свойства. Да предположим, че се натъкнах на проблема по следния начин:

Като се има предвид дължината на векторите и дължината на сумата на тези вектори. Да се ​​намери дължината на разликата между тези вектори.

Справяне с този проблем и други подобни, както и обяснение за това как да ги решим - в урока "добавяне на Вектори: сума на векторите в дължината и теоремата косинус".

И провери на решаването на тези проблеми могат да бъдат показани на калкулатора онлайн "неизвестен страна на триъгълника (добавяне на вектори и теоремата косинус)."

Когато продукти от вектори?

Продукт на вектор за вектор е нелинейни операции и разглежда отделно. И ние научихме "скаларно произведение на вектори" и "вектор и смесен продукт на вектори".

Проекцията на вектора на ос е равна на произведението на дължината на проектираното вектора на косинуса на ъгъла между вектора и оста:

Както е известно, проекция на точка А на правата линия (равнина) е подножието на перпендикулярно от тази точка на линията (повърхност).

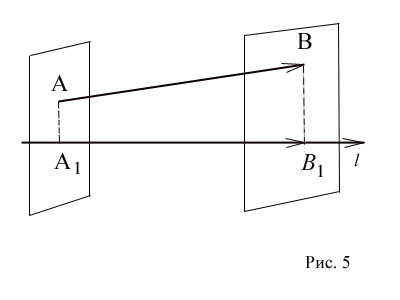
Да - произволен вектор (Фигура 5.) А и - прогнози началото му (точка А) и в края (точка Б) на л-ос. (За конструиране на проекция точка а) на линията през точката А провеждане равнина, перпендикулярна линия. Пресечната точка на линия и равнина ще определи желаната проекция.

L vektorana ос компонент се нарича вектор лежи на оста, в началото на който съвпада с проекцията на началото и края - края на вектора на проекцията на.

Проекцията на вектора на L-оста е броят

Дължина на вектор е равна на тази ос, взето със знак плюс, ако sostavlyayushey посока съвпада с посоката на оста л. и с отрицателен знак, ако те са в противоположни посоки.

Основните свойства на прогнозите на вектор на ос:

1. проекциите на вектори равни на една и съща ос, са равни.

2. Когато умножена по броя на вектор проекция се умножава по същия номер.

3. проекция на вектор сумата всяка ос е равна на сумата на издатъците при същите условия ос вектори.

4. проекцията на вектора на ос е равна на произведението на дължината на проектираното вектора на косинуса на ъгъла между вектора и оста:

Пример 3. Изчисляване на сумата вектор на проекцията на L-ос. ако и ъгли -

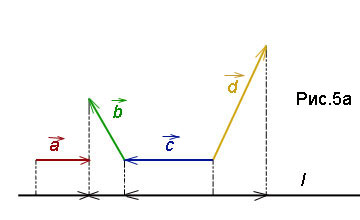
Решение. L проект векторите, както са определени по-горе в теоретична помощ ос. От fig.5a очевидно, че проекцията на вектор сумата е равна на сумата на проекциите на векторите. Ние изчисляваме тези прогнози:

Намираме се изисква проекцията на вектора на сумата от:

Познаването на правоъгълна Декартова координатна система в пространството проведе в съответния клас. е желателно да я отворите в нов прозорец.

Поръчаната система на координатни оси 0xyz Ox ос се нарича на хоризонталната ос. 0y ос - у-ос. и ос 0z - Z-ос.

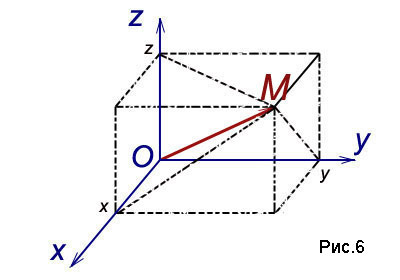
С произволна точка М асоциирано пространство вектор

нарича радиус вектора на точка M и да го прожектирате всяка от координатните оси. Означаваме стойности съответните издатини:

номера Х, Y, Z координати на точката се наричат ​​MA абсциса съответно. координират и applicate. и е писано в подредена запетая: М (х; у; Z) (Фиг.6).

Единичен вектор, чиято посока съвпада с посоката на оста, се нарича единичен вектор (или единичен вектор) ос. Ние означаваме с

Следователно, единични вектори на координатните оси Ox. Oy. Оз

Теорема. Всеки вектор може да се разлага от единичен вектор на координатните оси:

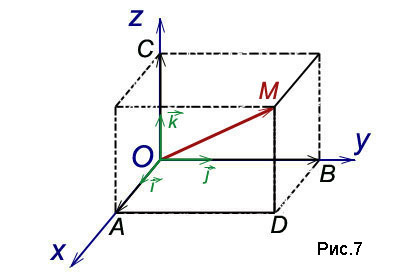
Уравнение (2) се нарича разпадане вектори по координатните оси. Коефициентите на това разширение са проекции на вектора на координатните оси. Така коефициентите на разширение (2) на вектора на координатните оси са координатите на вектора.

След като изберете конкретен пространство вектор координатна система и неговия произход тройна определи еднозначно помежду си, обаче, векторът може да бъде в писмена форма

Вектор представяне във формата (2) и (3) са идентични.

Както вече писахме, векторите се наричат ​​колинеарни, ако те са свързани с

Да предположим, че векторите. Тези вектори са колинеарни, ако координатите на векторите са свързани с

това е, координатите на векторите пропорционална.

Пример 4 Предвид вектори. дали тези вектори лежат на една права?

Решение. Нека да се определи съотношението на координатните вектори на данни:

Координатите на векторите пропорционални, следователно, векторите са колинеарни, или което е същото паралел.

п - мерни вектори и операциите по тях

В проучването на много въпроси, като например икономически, че е подходящо да се обобщи, обсъдени техники за преобразуване между цифри и точки на двуизмерни и триизмерни пространство и разгледа последователността на N реални числа като "точка" на някаква абстрактна "наш тримерно пространство", както и на самите числа - като " координира "от тези точки. За наш тримерно векторни компоненти могат да се данни, като производителността на различни култури, обемът на продажбите на стоки, технически фактори, от порядъка на стоките в складовете и т.н.

наш тримерно вектор е подреден набор от N реални числа записани под формата на

където - I - ия елемент (или I - та компонент) на вектора х.

Освен това има и друг запис вектор - под формата на колона координати:

Размерът на вектора се определя от броя на неговия произход и е отличителна характеристика. Например, (2, 5) - двумерен вектор (2, -3, 0) - триизмерен (1; 3, -2, -4, 7) - пет двумерен,

п - двумерен вектор.

Нулевият вектор е вектор, чиито координати са равни на нула:

Въвеждане на действието на N-двумерен вектори.

действителният брой е вектор

т.е. вектор като се умножи по броя на всяка координата се умножава с този номер.

можете да получите обратна вектор

т.е. чрез добавяне на векторите на същите размери на съответните координати termwise добавя.

Ако условията на продажбите на търговските предприятия продажби мрежа на стоки, определени като положителни нива на стоки и разходите за продажби - като отрицателна, ние получат разходите за векторни продажби

продажби (себестойност), к - м и продукт сега. и к = 1, 2, 3, ..., m.

обща цена вектора на продажбите се определя чрез добавяне на векторите на продажбите на всички м мрежовите компании у разходи:

Сумата от противоположни вектори дава нулев вектор:

При изваждане на два вектора на същите размери на съответните координати се изважда срок от термин:

Манипулиране н тримерно вектори отговарят на следните свойства.