Подготовка на учениците за изпита и OGE (ДПА) в резолюцията на център за обучение (наръчник по математика -
Съществуването на окръжност вписана в триъгълник
1. Определяне на ъглополовящата на ъгъл се нарича лъч, който разделя ъгълът на две равни части.
Теорема 1 (Основно свойство ъглополовяща). Всяка точка на ъглополовящата на ъгъла е на еднакво разстояние от стените на ъгъла (Фиг.1).

Доказателство. Г. Помислете произволна точка лежи на ъглополовящата на BAC на ъгъл. и капка от точка D DE и DF перпендикулярите към страните на ъгъла (Фиг.1). Ъгловата триъгълници ADE и ADF са равни. защото те са остри ъгли DAF и DAE. и хипотенуза АД - общо. Ето защо,
QED.
Теорема 2 (обратна теорема теорема 1). Ако една точка се намира на еднакво разстояние от двете страни на ъгъла. Тя се намира на ъглополовящата на ъгъла (Фигура 2).

Доказателство. Помислете за произволна точка Г. лежи в рамките на БКК на ъгъл и се намира на еднакво разстояние от двете страни на ъгъла. Капка от точка D DE и DF перпендикулярите към страните на ъгъла (Фигура 2). Ъгловата триъгълници ADE и ADF са равни. защото те са краката на DF и DE. и хипотенуза АД - общо. Ето защо,
QED.
2. Определяне кръг е кръг вписан ъгъл. ако тя засяга страните от ъгъла.
ТЕОРЕМА 3. Ако кръгът е вписан под ъгъл, разстоянието от точките на върховете на допирателната към окръжност с ъгъл равен страни.
Доказателство. Нека точка D - център на кръга, вписан в ъгъла на BAC. и точки Е и F - точка на допиране кръг с ъгъл страни (Фигура 3).

QED.
Забележка. Теорема 3 може също така да бъде формулирано по друг начин: допирателна дължини. извършва към обиколката на една точка, са равни.
3. Определяне на ъглополовяща на триъгълника се нарича сегмент, който е част от ъгъл ъглополовяща на триъгълника, а триъгълника се присъедини към връх до точка, от другата страна.
Теорема 4. Във всеки триъгълник, и трите ъглополовяща се пресичат в една точка.
Доказателство. Помислете два ъглополовяща проведено от върховете А и С ABC триъгълник. и означават точката на пресичане с буквата О (фиг. 4).
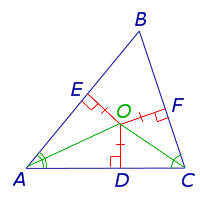
Капка от точка O вертикалите OD. OE и от страна на триъгълника. Тъй като точка O лежи на ъглополовящата на BAC ъгъл. след това от Теорема 1 равенство:
Тъй като точката О лежи на ъглополовящата на АТБ ъгъл. след това от Теорема 1 равенство:
Вследствие на това равенство:
откъдето с помощта на Теорема 2, ние заключаваме, че О лежи на ъглополовящата на ъгъла ABC. По този начин, всички три триъгълник ъглополовяща преминава през една и съща точка, както се изисква
4. Определяне на окръжност вписана в триъгълник. Това е кръг, който засяга всички страни на триъгълника (Фигура 5). В този случай, на триъгълника се нарича триъгълник, кръг, описан за.
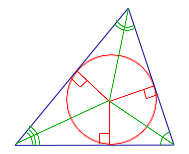
Следствие. Във всеки триъгълник окръжност може да се впише, и само един. Център на кръг вписан в триъгълника е точката, в която всичко се пресичат ъглополовящи на триъгълник.
Формулата за радиуса на кръга вписан в триъгълник
Формула Ви позволява да намерите на радиуса на окръжност вписана в триъгълника. удобно представени в таблицата по-долу.