Площта на триъгълника чрез областта ограничена кръг - с формула, изчисляване пример

Предишен ◈ Следващото

А триъгълник се нарича с надпис, ако всички негови върхове лежат на кръга. В този случай, кръгът се нарича описана около триъгълника.

Площта на триъгълника чрез областта ограничена кръг - с формула, изчисляване пример

Разстоянието от центъра на върховете на всеки триъгълник е един и същ и е равна на радиуса на този кръг. Около всеки триъгълник може да се опише като кръг, но само един.

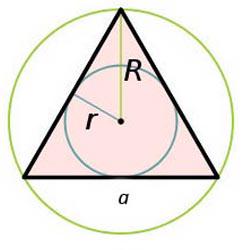
Окръжност ще лежи в пресечната точка на midperpendiculars държани от всяка страна на триъгълника. Ако кръгът е описан около правоъгълен триъгълник, чийто център ще се намира в средата на хипотенузата. За всеки триъгълник, кръга, описан около който действа формула триъгълник области от радиуса на окръжност кръг:

където А, В, С, - страна на триъгълника, и R - радиусът на кръга.

Пример за изчисляване на триъгълника на радиуса на окръжност кръг:
Нека триъгълник със страни а = 5 см, б = 6 см, с = 4 cm. Около описва окръжност с R = 3 см. Вземете област.
Като се изисква всички данни, просто замени стойностите във формулата:

площ на триъгълник е равен на 10 квадратни метра. виждам

Доста често могат да отговарят на условията на тази област на описаните окръжности, които да се използват за намиране на триъгълник вписан квадрат. Формула триъгълник област чрез площ ограничена кръг е след изчисляване на радиуса. Тя може да се изчисли по няколко начина. Първо, помислете за формулата за района на кръг:
Да превърнем тази формула, ние откриваме, че радиусът:
С помощта на тази формула, ние откриваме, че познаването на района на описаните окръжности, площта на триъгълник може да се намери по следния начин:

Знаейки трите страни на даден триъгълник може да се използва, за да намерите областта на формула на Херон. Тъй като това е възможно да се намери радиуса на описаните окръжности. Това означава, че ако условията са всички страни на триъгълника и на площада се налага да търси чрез радиуса на кръга, първо трябва да го изчисли по следната формула:

Това означава, че познаването на дължините на страните на триъгълника, можем да намерим областта на триъгълник от радиуса на кръга.

Пример за изчисляване на триъгълника чрез площ ограничена кръг:
Дан триъгълник около който да описва окръжност с площ от 8 квадратни метра. Страните на триъгълник см а = 4 см, В = 3 см, с = 5 см, за да намерите началото радиусът на кръга от площта му ..:

Нека се опитаме да намерим радиуса с друга формула, която сме произлиза от начина на намиране на площта на триъгълник от три страни. Semiperimeter ще намерите:

Заместването стойности във формулата:

Сега ние използваме формулата за намиране областта на триъгълник вписан:

Знаейки няколко прости формули, ние бяхме в състояние да се намери областта на триъгълник вписан. Тя ще бъде равна на 6 кв. см.