Математика за блондинки диагонални на правоъгълен паралелепипед

Това е, което аз бях помолен интересен въпрос: как да намерите на обема на правоъгълен паралелепипед, знаейки, трите си диагонали, които излизат от един връх? Първата ми мисъл - да се копае в математическия наръчника. Но любимата ми справка мълчи. Има и друг извор на мъдрост - Уикипедия. Страницата на руски език на правоъгълен паралелепипед, впечатлява със своята мизерия. теорема Дори Питагор за триизмерното пространство не е там. Обикновено в такива случаи, когато включвам точно една и съща страница на английски език. В крайна сметка, математиката - това е едно от нещата, които не се нуждае от преводачи. Най-често, има много повече различни формули. По това време аз бях в очакване на голямо разочарование. Да, видях там Питагоровата теорема за правоъгълен паралелепипед. И все пак. Всяка математическа боклук в насипно състояние Уикипедия, но най-интересното там. Pechalka.

Нека се опитаме да мисли логично. Ако някой се запита подобен проблем, след решението на този проблем е. Нашите математика все още не са узрели до точката, където учениците си признават неговото незнание на нещо. Това ли е най-смелите. Останалите глупаво повторя това, което им се е научил веднъж. Това предполага, решението: съставяне на Питагоровата теорема за три диагонални ръбове, да ги комбинирате в система от три уравнения с три неизвестни, реши и да намерят размерите на правоъгълен паралелепипед. Брррр! Ужас.

Сега мислим от другата страна. Обем - резултат от умножението на дължината на трите измервания. Имаме три диагонал дължина. Теоретично може да се получи сумата. Нека да се направи нашата диагонал на правоъгълен паралелепипед, и да видим какво можем да направим с тях. Погледни от различни ъгли, за да стане ясно.

На снимката е осветена в синьо правоъгълен паралелепипед тези елементи, които са известни за нас. Това диагонални ръбове. Red подчерта факта, че ние не знаем. Дали диагонала на правоъгълен паралелепипед, както и неговите линейни размери (като математика все още ги наричат ​​размерите карето). О, и огромният обем от нас също не са известни.

Сега, въоръжени с древна питагорова теорема дядо и пишат размерите формула и диагоналите. Кутия имаме правоъгълна, тогава всички ъгли между линейните размери и прави ръбове. Ние не забравяме, че основната ни цел - да намери силата на звука.

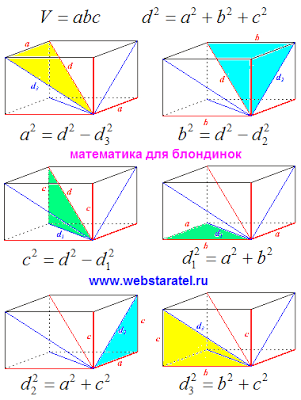
Снимки от множество разсее формули. Пишем формула отделна купчина. Математика в този случай мъдро говори за "много математически формули." Ние разглеждаме формулата и се опитват да най-малкото нещо да се мисли. Ние трябва да се отървете от измерване и диагонала на правоъгълен паралелепипед, защото те не са ни известни. Сега, ако диагонала на полето, изразена по отношение на диагонала странични лица. Много много формула в дясната половина на шепа подобни един на друг.

Има! Диагонал на квадратните лица са две квадратчета по диагонал кутия. Сега, съвсем просто. Както блокове в детска градина. Премахване на скоби, добавете скоби. И ние получаваме формулата.

След това, полученият формула е заместен в формула с линейни размери и получаване на експресионни линейни размери чрез диагоналните лица. След това записва обемът на формула.

Всичко. Проблемът е решен. Резултатът е много красива и елегантна формула. Сумата от квадратите на двата диагонала на квадрата лицата изважда трето лице. След това се умножава, дели на осем завои квадрат обем на правоъгълен паралелепипед. Аз разбирам, че това е една от основните свойства на пространството. Използване на принципа на прегрупиране и кофактори условия могат да бъдат показани подобни формули за многомерни пространства с произволен брой размери. Всяко мултивариантен обем може да бъде изразена по отношение на елементи с по-малък брой измервания. За съжаление, ние правим по математика за това не казвай нищо. Или те не знаят нищо, или срамежлив. Но лишена от каквито и да било проблеми, които са толкова любители на нашите учители пред нас красотата на математиката в първоначалния си вид.