Математика за блондинки диагонални, кутия и диамант
Ето едно предизвикателство. Причината е правоъгълен паралелепипед ромб, чиято страна е равна на 6 см, а ъгълът на 60 градуса. Височината на паралелепипеда е равна на 8 см, получавате дължината на по-късия диагонал на паралелепипеда.
Ние започваме да се говори. Кутия и диамант на дъното - това е като една малка кутийка, която е подобна на горната част на диаманта. Такава паралелепипед наистина възможно да се направят две диагонални двойки, дължината на които ще се различават. От горе до долу в остър ъгъл с горната остър ъгъл връх може да побере един дълъг диагонал. Но тъп връх (не в смисъл, че тези върхове не разбират, но в смисъл, че тези върхове prihvatizirovat тъпи ъгли) ще бъде свързан с къси диагонали. Тези два диагонала, те са с еднаква дължина. Вижте снимката, тя изглежда като един от тези диагонали.
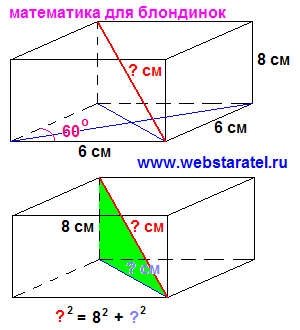
Диагонала на правоъгълен паралелепипед, показан в червено, диагонала на основата ромб показват в синьо. Ако се опитате много трудно да се простират въображението си и да се вгледате внимателно в снимката по-горе, ще видите, правоъгълен триъгълник. Кутия ние правоъгълни. Това означава, че страничният ръб е разположен под прав ъгъл към основата. Диагонала основа (sinenkaja), диагонал на паралелепипед (червено) и ребро (Chernen'kii, подчертавайки, не успя да прикрие фризьора) образува правоъгълен триъгълник. И когато има правоъгълен триъгълник, където царува древния питагорова теорема. Винаги, без значение кой си в страната избира цар или президент.
В долната част, под снимката, написан този много известен теорема прилага за нашия случай. Не се изненадвайте, ако по този начин да се запознаем Питагоровата теорема за първи път. На първо място, не всички се научили с вас в един и същи клас, и те не могат да се знае точно колко сте били обучен правилно записване на питагорова теорема. На второ място, в теоремата на Питагор най-важното не е приет от някой zakoryuchek система и смисъл - да отнеме две перпендикулярни неща, квадратура, в купчина и да получите трета Thing на квадрат. Имаме квадратни ръбове и диагонали на ромб квадрат chudnenko сгъната в квадратен паралелепипед диагонал.
Сега ние трябва да се справят с диагонал на ромба. Ние приемаме нашата кутия с форма на правоъгълен паралелепипед, отворете капака и гледам вътре. Защо гледаме вътре в кутията и не учат самия капак? Тя работи безотказно любопитна маймуна теорема. Опитайте нещо да се копае и погледнете вътре. Защо тогава се отвори. Всеки, дори и неграмотен, математик ще ви кажа, че теоремата изисква доказателство. В един момент. Попитайте майка си, за да си купиш нещо в кутия. Когато тя ще го доведе до вас, вие, с очите си затворени, отворете капака на кутията, а самата кутия, без да се обръща, хвърли в кошчето. То не е работа? Всички теорема.
Всички наши кутия е празна и ние можем да проучи внимателно фундамента. Тя има форма на диамант, който може да се извърши по диагонал. При пресичане, тези диагонали представляват chudnenko триъгълници. Вече четири от тях. Ние не сме алчни хора, имаме само един. Какво знаем за триъгълници (на снимката по-долу той е боядисан в прекрасен цвят)? Този триъгълник не е точно Бермуда, а не обичам. И какво от това? Ние се изкачи до интернет и търсят свойства на диаманта. Имаме ги веднъж преподава в училище, но това беше толкова отдавна. Интернет е пълен с глупости, но има и нещо нещо интересно за нас. Всички страни на ромба са едни и същи. Диагоналите на ромб са различни. Стискайте диагонално под прав ъгъл. Пресечната точка на диагоналите ги разделя на две равни половини. Всяка диагонал разделя ъгълът при върха равни (у ромбове и площади диагонално не алчни). Изглежда всичко. Други неща за диамант модел не ни интересуват.
И така, в резултат на нашите изследвания, ние открихме, че нашата триъгълник е правоъгълна. Хипотенузата е равна на дължината на неговата страна на ромба, краката са равни половини на диагоналите. Отново се опита на дядо си Питагор. Дължината на хипотенузата знаем, но с двата крака на проблема. Някои мързелив не се притеснява да се измери диагонала. Но това чудо е успял да изчезнат от ъгъла, под връх. В традиционната форма на питагорова теорема не се търкаля (това не е печатна грешка, то е в смисъл на "не е подходящ"). Остава само да тригонометрията. Тя също така работи в правоъгълен триъгълник, но тя излезе с математиката изключително за мними деца. Лично аз мисля така. Мисля, че тази идея ще доведе до не малка група от Vkontakte. "Мразя тригонометрия" - измислено име за групата, давам.
Как да разберете указанията на лекаря за използването на тригонометрията е невъзможността за използване на питагорова теорема заради липсата на двама от сумите триъгълника и стойността на един от ъглите. Ако ние не разполагаме с ъгъл, след което лекарството ще бъде безсилна. Как да кандидатствате тригонометрия? Ние няма да излъскване на Интернет, аз ще ви покажа по-надежден инструмент. Нарекох го "портрет на тангента". Ние го постави на върха на триъгълника, ъгълът, под който е известно, че с нас. Хоризонтална прът разположен успоредно на линията, от която смятаме ъгъла (имаме хоризонтална диагонал). Тогава си спомням, "Tangent - е синуса и косинуса." Външен пръчка портрет означава синуси, ниски коли - уют. Трябва да намерим вертикалния крак на триъгълника. Така че, това хипотенуза да бъде умножен по синуса на ъгъла. Ако имахме нужда от хоризонтален крак, ние ще се умножава по косинус на същия ъгъл. По цялата дължина на вертикалната диагонала на ромба (sinenkaja) е установено, че два пъти дължината на крака на триъгълник.
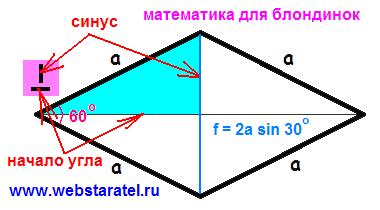
Всичко. Задачата сме разбрали. Определяне на диагонала на буквата ромб "е", далеч - от буквата "а", ъгълът - ". Алфа" буквата Диагонал на кутията, ще бъдат обозначени с буквата "г", а надморската му височина - буквата "ч". Сега пиша формулата за решението, заместваме в тях, че ние знаем, ценностите и да получите резултат.

Дължината на малък диагонал е установено, че е 10 cm. Можете, разбира се, се изчисли дължината на дългия диагонал, но любопитна маймуна теорема в този случай, тя отказва да работи. Тя (теорема) знае, че няма нищо вкусно или интересно, в резултат на изчисленията, които получаваме.