Линейна функция на неговите свойства и график

където к и б са реални числа.

Свойства на линейната функция

Linear функция има следните свойства:

1. у = KX + б - тя може дори или нечетен функция;






2. домен на функция Y = KX + б - цяло число линия;
3. Наборът от стойности на линейната функция - цялата реална линия;
4. Ако к е по-голяма от 0, увеличава функционалните и ако к е по-малко от 0, тогава линейна функция намалява.

Наклонът на линейната функция

Коефициент к във формулата на линейна функция е наклонът.

Наклонът се определя ъгълът между графиката на линейна функция и положителната посока на оста х.

Графиката на линейна функция

Графиката на линейна функция е права линия. Тук е у = 2х + 1 линейна функция графика

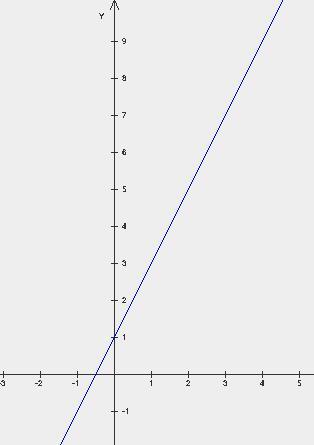
Тук на наклона е по-голяма от нула, ъгълът на линия у права = 2х + 1 с оста х положителна посока - остра.

Сега нека да видим как се променят графика на линейна функция Y = 2x + 1, ако наклонът направи отрицателен, т.е. у = -2x + 1

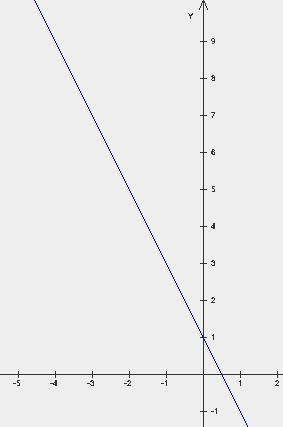
Тук ъгълът линия у права = -2x + 1, положителната посока на оста х - тъп.

Като линейна функция графика се променя в зависимост от броя на б във формулата на линейна функция у = KX + б? Ако б увеличение, графиката се премества нагоре, ако намаляването на броя Ь, у = графика KX + б движи надолу.

Графиката на линейната функция Y = KX + б, можете да се изгради сега с помощта на съставителя на графици. Изберете я под формата на функция "Line: у = к * х + б" и натиснете бутона "заговор". Извършване на експерименти: настройте ъглови съотношения по-голямо и по-малко от нула, промяна на стойностите на б и да видим как ще се промени графиката на линейната функция.