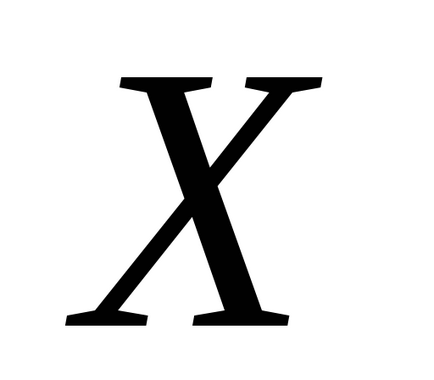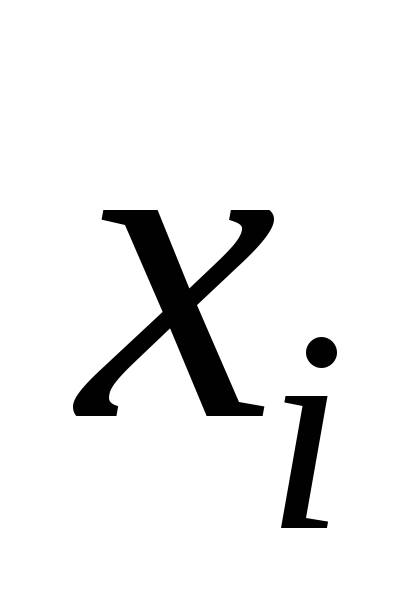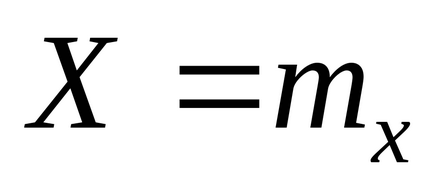Чрез числените характеристики на случайни величини включва: очакване, дисперсия, моменти на различни поръчки и т.н.
нека
- дискретни случайни величини приема стойности
с вероятности
съответно.
Очакване (ST) или средната стойност DM
е броят
на предположението, че серията клони абсолютно.
Ако броят
отклонява, тогава ние казваме, че SV
Той има краен во
ако
- непрекъснати случайни величини с вероятност плътност
, след това го во определя от интеграла
при условие, че се доближава абсолютно.
нека
- дискретни случайни величини с право на разпределение (2.1) (Относно: скаларни случайни величини) и
- функция на RV Тогава законът на разпределение на случайни величини
Той има формата на таблица. 7.1 (Subject: Скаларни случайни величини). Според уравнение (1.1) ва случайна променлива
определя по формулата
.
Ако, обаче,
- непрекъснати случайни величини с вероятност плътност
, че генерализиране предишните аргументи, ние се получи формула за МО случайна променлива
под формата на
Пример 1.1. Паричните средства за томболата на 200 издадени билети. Играна печалба в размер на 50 рубли. две - до 25 рубли. десет - 1 втриване. Намерете средната стойност печалба, ако е купил един билет.
Съгласно пример D 2.1 (Относно: Скаларни случайни стойности) разпределение право D.S.
- победа - това е (2.2) (Относно: Скаларни случайни величини).
Съгласно формула (1.1), средната стойност за спечелване
Така, средната печалба в лотарията е равно на 55 копейки. ▲
Пример 1.2. функцията на плътността на вероятността на случайни променливи
външност
Според формула D (1.3)
. ▲
Нека обясним основните свойства на очакването.
1 0. MO на броя на повторения на събития
в един тест еднаква вероятност
това събитие.
2 0. MO неслучайно постоянна стойност
е
.
3 0. Constant множител неслучайно
Може да се приема като знак на очакването.
4 0. За всички случайни променливи (зависим или независим) ва количество SV
и
равна на сумата MO тези стойности:
5 0. За независими случайни величини-ви произведения SV
и
равна на произведението на ст на SV т.е.
Пример 1.3. Намери MO сумата от броя на точките, които могат да падне, когато хвърлят два зара.
Нека D
и
- броят на спада точки от първия и втория костите, съответно. Дискретни случайни величини
и
вземат стойности 1, 2, 3, 4, 5 и 6 с еднаква вероятност
. След това от (1.4) и (1.1), необходими MO
. ▲
MO Тя характеризира DM средната стойност SV отклонение
от неговото математическо очакване (средно) .. Често наричан стойността на SV
nazyvaetsyatsentrirovannoy SV
Дисперсия или разсейване
случайна променлива
Това е математическото очакване на квадратен отклонение на случайната променлива
от неговото математическо очакване:
Корен квадратен от дисперсията се нарича средната квадратична (квадратичен) отклонение D.S.
и е означен
, така че
.
За дискретни случайни величини
, приема стойности
вероятност
,
, дисперсия се определя от уравнението
За непрекъснати случайни величини
дисперсия се определя от уравнението
ако съществува тази интегрална. тук
- дм вероятност плътност
.
От свойствата на ММ и определяне на дисперсията имат
.
Така че, за дискретни случайни величини
За непрекъснати случайни величини
(2.4) има формата
Формули (2.4) и (2.5) са по-удобни за изчисляване на дисперсията.
Забележка. От дефиницията на дисперсия (2.1) D.S.
следва, че
. Ако отклонението е малка, тогава всеки период от сумата (2.2) е малък. Ето защо, стойността
, в която
голям, трябва да има малка вероятност. С други думи, с малък дисперсионни големи отклонения сухото вещество
от нея MO
малко вероятно. равенство
означава, че
за тези стойности
, вероятност
е равна на нула. С други думи,
означава, че
с вероятност единство.
Пример 2.1. Намери разсейването на автобуса
, даден закон на вероятностно разпределение