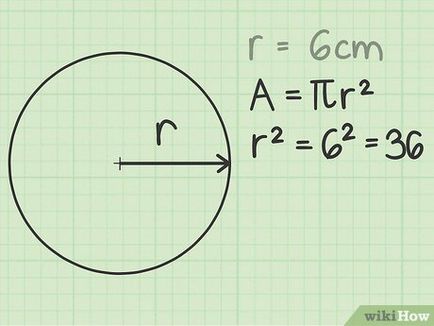
Намерете радиуса на кръга. Радиус - сегмент, който свързва центъра на кръга за всяка точка от външната периферия на кръга. Радиусът може да се измерва във всяка посока, би било същото. Радиусът е равен на половината от диаметъра на окръжността. Диаметър - е сегмента, която преминава през центъра на кръга и свързва две точки на външната периферия на кръга. [1]
- Като правило, стойността на радиус, дадена в проблема. Доста трудно да се намери точно в центъра на кръга, освен ако не е маркиран в кръга, който се съставя на хартиен носител.
- Например, радиусът на кръга е 6 см.
Повдигнете радиуса на квадрат. Формулата за изчисляване на площта на кръг: S = π R 2>. където R - радиус, който е издигнат на втора степен (квадрат). [2]
- Няма нужда да се изпъна цялата формула.
- В нашия пример: R = 6. Следователно R2 = 36 = 36>.
Полученият резултат се умножава по броя Pi. Този номер е обозначен с гръцката буква П и е математическа константа, която характеризира отношението на радиуса на кръга и на площада. Pi е приблизително равна на 3,14. Точната стойност на Пи включва неограничен брой цифри. Понякога отговор (площ на кръг), записани с постоянен π. [3]
- В нашия пример (R = 6 cm) квадратен се изчислява както следва:
- S = π R 2>
- S = π 02 юни>
- S = 36 и S = π 36 (3. 14) = 113. 04
Напишете отговора. Не забравяйте, че районът се измерва в квадратни единици. Ако радиусът е даден в см, площта в квадратни сантиметра. Ако радиусът се дава в милиметри, площ, измерена в квадратни милиметри. Консултирайте се с инструктор, независимо дали искате да представи отговор на постоянно П, или в цифрова форма, като се използва приблизителна стойност на пи. Ако търсенето не е ясно, запишете на двете отговорите. [4]
- В нашия пример (R = 6 cm) S = π 36 cm 2 или S = 113,04 cm2.
Запишете превръща формула. Ако е известна продължителността на обиколката на кръга, можем да използваме формулата за изчисляване на трансформира своята област. Тази формула включва периферен дължина и радиус не са, и се изписва така:
Измерете и запишете на окръжността. В някои ситуации, не е възможно да се измери точно на диаметъра или радиуса. Ако диаметърът не е съставен или център, не е маркирано, че е много трудно да се намери точно в центъра на кръга. Обиколката на определени предмети (напр тигани) е доста лесно да се измери с ролетка, е възможно да се намери по-точна стойност на обиколката от диаметъра. [5]
- Например дължината на обиколката на окръжността (или кръг обект) е 42 cm.
Използва се съотношение между дължина и радиус на окръжността на презапис. Обиколката е равен на броя на Пи диаметър. Тя може да се запише като: C = π г. Припомнете си, че диаметър, равен на два пъти радиуса, т.е. г = 2 R. Комбинирайте тези уравнения, да изгори следната формула: C = π 2 R. Сега изолира променлива г. [6]
- С = π R 2
- C 2 π = г> = R> (разделят двете страни от 2 π)
Запишете формулата за изчисляване на площта на кръг. Запишете превръща формула базата на съотношението между дължината и радиуса на кръга. Заместител последното равенство в стандартната формула за изчисляване на площта на кръг: [7]
- S = π R 2> (стандартна формула)
- S = π (С 2 π) 2>)> (вместо рамка експресия с)
- S = π (С, 4-ти февруари π 2) >>>)> (издигната в квадрат фракция)
- S = C 02 април π >>> (π намалена в числителя и в знаменателя)
Използвайте превръща формула за решаване на проблема. Сега във формулата вместо от радиуса на окръжността е налице, поради което е възможно да се изчисли областта на кръг от известен обиколка. Поставете стойност по дължина на обиколката и извършване на изчисления, както следва: [8]
- В нашия пример, С = 42 cm.
- S = C 02 април π >>>
- S = 42 02 април π >>> (рамка стойност)
- 1764 S = 4 π >> (изчислен 42 2)
- S = 441 π >> (разделена на четири)
Напишете отговора. Ако дължината по периферията е дадено като число, а не продукт на броя и П. отговорът може да се запише π в знаменателя. Или вместо Pi замени приблизителната му стойност (3.14). [9]
- В нашия пример (С = 42 cm) S = π >> 441 cm2.
- Или като: S = 441 π = 441 3. 14 = 140. 4> => = 140.4> cm2.