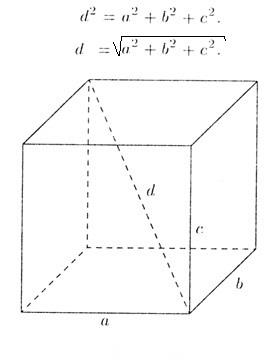
диагонал на паралелепипеда

Диагонала на правоъгълен паралелепипед - сегмент свързването му противоположни върха. Така че, ние имаме форма на паралелепипед с диагонал г и със страните, а, б, в. Едно от свойствата паралелепипед посочва, че квадратен диагонал дължина D е равно на сумата от квадратите на неговите три измерения, а, б, в. Следователно заключението, че диагонала може лесно да се изчислява по следната формула:

Ако правоъгълен паралелепипед известна дължина, височина и ширина (а, б, в) формулата за изчисляване на диагонала ще изглежда по следния начин:

Учителите обикновено не предлагат на своите ученици "празна" формула, и полагат усилия, така че те могат да го носят сами чрез задаване на подвеждащи въпроси:

• което трябва да знаете какви данни имаме?
• който разполага с правоъгълен паралелепипед?
• се прилага независимо дали питагорова теорема тук? Как?
• дали има достатъчно данни, за да се приложи питагорова теорема или нужда от някои други изчисления?

Обикновено, след като отговор на тези въпроси, учениците могат лесно да заключим тази формула сам.

Един правоъгълен паралелепипед е един от така се наричат ​​polyhedra, която се състои от шест страни, всяка от които е правоъгълник. А диагонал - сегмент, който свързва противоположни върховете на успоредник. Ако дължината, ширината и височината на правоъгълна паралелепипед приема като А, В, С, съответно, след това с формула диагоналите (D) е както следва: D ^ 2 = а ^ 2 + б ^ 2 + C ^ 2.