линейна функция

Линейна функция е функция, определена от формулата у = KX + б. където к и б - някакви реални числа.
Графиката на линейна функция е права линия.

Ако к = 0, тогава функция у = б се нарича константа. график й е линия, успоредна на оста Ox.
Ако б = 0, тогава формулата у = KX определя директно пропорционална. Графиката на такава функция е права линия, минаваща през произход.

Обратното е вярно - всяка линия, не успоредна на оста Oy. Това е графика на линейна функция.

к, който се нарича номер на наклона на линията. е равна на допирателната на ъгъла между правата линия и положителната посока на оста Ox.
Фигура - ъгъл # 945;.

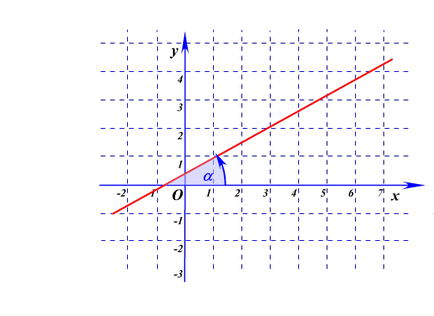
Построява се графика на линейна функция е лесно.
Позицията на всеки ред е еднозначно определена от нейните две точки. Следователно, линейна функция е напълно определена чрез определяне на неговите стойности за двете стойности на аргумента. Например,

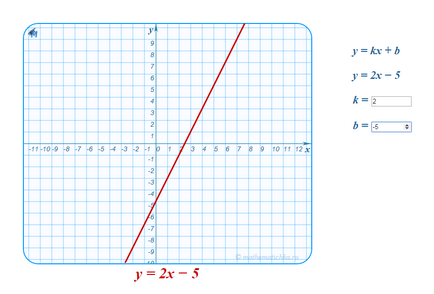
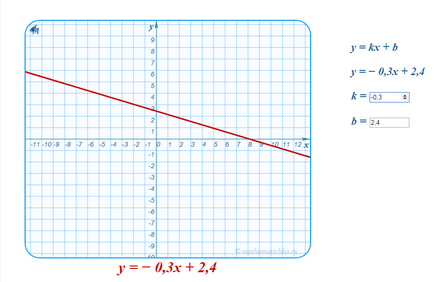
Ако сте мой студент, или абонат. можете да работите с интерактивни версии на тези графики.

Свойства на линейната функция на к ≠ 0, б ≠ 0.
1) областта на функцията - множеството на всички реални числа: R или (-∞; ∞).
2) у функция = KX + б е дори аудио или нечетен.
3) Ако к> 0, функцията увеличава монотонно и ако к