Еластичност на функция - studopediya

Производни на по-висок ред

Тъй като производно на самата функция е функция, то може също така да бъдат получени. Концепцията на производно, което е дискутирано по-горе, се отнася до производно на първия ред.

Производно на N-ти ред е производно на производното
(М - 1) -ти ред. Например, е `` (х) = (е `(х))` - производно от втори ред (или втора производно), е `` `(х) = (f`` (х)) `- производно на третия ред (или трето производно) и т.н. Понякога за означаване производни с по-висок порядък се използват римски или арабски цифри в скоби, например, F (5) (х) или е (V), (х) на производното на пети ред.

Физическата смисъла на високи производни ред, определен по същия начин, както за първата производна: всеки от тях представлява скоростта на промяна производно на предходния ред. Например, втората производна е степента на промяна на първия, т.е. скорост скорост. За праволинейно движение е ускоряване точка във времето.

Еластичност функция Ex (у) се нарича граница на съотношението на относителното нарастване на функцията на относително увеличение на аргумент х, последният клони към нула :.

Еластичност функция показва приблизително, на процентна промяна функция у = F (х) с независими променливи х промени от 1%.

От икономическа гледна точка, разликата между този индекс на производното, че производното има единици на измерване, и следователно, неговата стойност зависи от блоковете в която измерената променлива. Например, ако зависимостта на производството на периода от време, се изразява в тонове, съответно, и месеца, производната ще покаже лимит увеличение на тона на месец; ако мярката тези показатели, например, в килограми и ден, и самата и нейната производна функция ще бъдат различни. Гъвкавостта е също по същество безразмерна величина (измерен в проценти или фракции), и следователно не зависи от мащаба на цени.

Основни теореми за диференцируеми функции и техните приложения

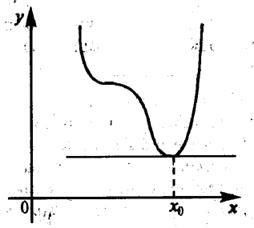
теорема на Ферма. Ако интервал диференцируема функция достига най-високата или най-ниската стойност на вътрешния точка на педя, производна на функцията в този момент е нула.

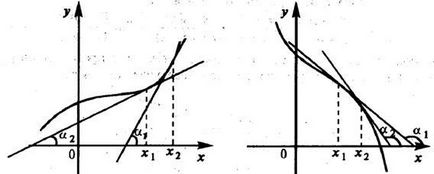
Геометричната смисъла на теоремата на Ферма състои в това, че на мястото на най-голям или поне стойност постигната в интервала, допирателната е успоредна на графиката на абсцисата (фигура 3.3).

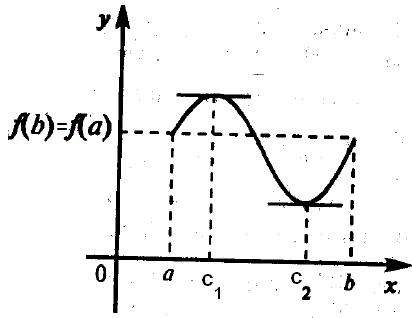
теорема Рол е. Нека функция у = F (х) отговаря на следните условия:

1) непрекъснато в интервала [а, Ь];

2) е диференцируема в интервал] а, Ь [;

3) в крайните точки на равни стойности, т.е. е (а) = F (б).

След това, в рамките на сегмент има най-малко една точка, при която функцията производно е нула.

Геометричната смисъла теорема Rolle е, че съществува най-малко една точка, при която допирателната към графиката на х-ос е успоредна на (например, на фигура 3.4 две такива точки).

Ако е (а) = F (б) = 0, Rolle теорема може да бъде посочено по друг начин, между две последователни нули диференцируема функция има най-малко една нула на производно.

теорема Рол е частен случай на теоремата на Лагранж.

теорема на Лагранж. Да приемем, че функция у = F (х) отговаря на следните условия:

1) непрекъснато в интервала [а, Ь];

2) е диференцируема в интервала (а, Ь).

След това в сегмента има най-малко една точка с, в kdtoroy производно е равно на отношението на нарастване на функцията на нарастване на аргумента на този сегмент :.

За да се разбере физическия смисъл на теоремата на Лагранж, ние се отбележи, че няма нищо по-високо от средното ниво на функция промяна на интервала [а, б]. По този начин, на теоремата казва, че в рамките на този сегмент има най-малко една точка, в която "моментната" темп на изменение на функцията е равна на средната скорост на изменение в целия сегмент.

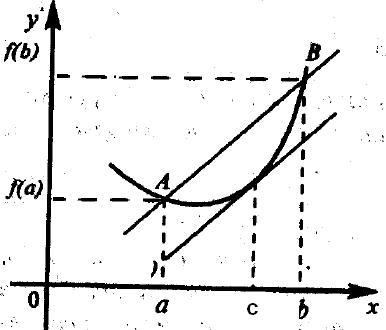
Геометричната смисъла на теоремата на Лагранж се илюстрира фигура 3.5. Имайте предвид, че изразът е наклон на линията, на която се намира на акорд КБ. В теорема гласи, че функцията на графиката, има най-малко една точка, в която допирателната към нея е успоредна на тази хорда (т.е., на наклона на допирателната - производно на - ще бъде същото).

Следствие: ако производното е нула на някои интервал, след това функцията идентично константа на този интервал.

В действителност, да поеме този интервал [а, Ь] интервал [а, х]. От теоремата на Лагранж в този интервал има точка с, за които. Следователно е (а) - е (х) = F `(а) (а - х) = 0; е (х) = F (а) = конст.

правило L'болницата. Границата на съотношението на два безкрайно малки или големи безкрайно функции е равна на границата на съотношението на техните производни (крайни или безкрайни), ако то съществува в този смисъл.

С други думи, ако има несигурност на формата, а след това.

Прилагането на правилото L'Hopital да намери границата той ще бъде прегледан в практически упражнения.

Достатъчно условие за увеличаване (намаляване) функция. Ако производно функция диференцируема положителния (отрицателен) в рамките на определен период от време, а след това се увеличава функция (намалява) в този интервал.

Доказателство. Да разгледаме две стойности X1 и X2 от даден интервал (например, x2> х1). Чрез теорема LaGrand на [x1. x2] има точка от където. Следователно е (х2) - е (х1) = F `(в) (х2 - х1). Тогава за е `(в)> 0, лявата страна на неравенството е положителен, т.е. F (х2)> е (х1), и функцията се увеличава. Когато е `(в) <0 левая часть неравенства отрицательна, т.е. f(х2 )

геометрични тълкуване функционални условия монотонност: ако тангентата към кривата на определен интервал са ориентирани на остри ъгли спрямо хоризонталната ос, увеличава функционалните и ако най-тъп след това намалява (виж фигура 3.6.).

Забележка: Предпоставка за монотонността на по-слабите. Ако се увеличава функцията (намалява) в определен интервал, то производно е неотрицателно (не-позитивни) в този интервал (т.е., в отделни точки деривати монотонни функции могат да бъдат нула).